8.7. The Natural Logarithm

This part deals solely with the reciprocal function

X^{- 1}

with a special emphasis on the primitive problem: Up to now we know primitives for all power functions, except this one. But as the reciprocal function is continuous there must be a primitive, at least on intervals according to [8.1.5].

Using the fundamental theorem [8.2.13] we now assign a special name to one of its primitivs on $ℝ^{> 0}$ .

Definition: The function $\ln : ℝ^{> 0} \to ℝ$ given by

\ln (x) ≔ \int_{1}^{x} \frac{1}{X}

[8.7.1]

is called the (natural) logarithm or the (natural) logarithm function.

Consider:

The name $\ln$ abbreviates the latin logarithmus naturalis.
Similar to the trigonometric functions it is common practise to write $\ln x$ instead of $\ln (x)$ .
The lower limit 1 in [8.7.1] arranges the value $\ln 1 = 0$ .

As a primitive of $\frac{1}{X} | ℝ^{> 0}$ ln is already differentiable and $\ln^{'} = \frac{1}{X} | ℝ^{> 0}$ . But from that we see that in fact ln is arbitrary often differentiable, $\ln \in C^{\infty} (ℝ^{> 0})$ , and continuous ([7.5.2]) as well.
Being continuous, $\ln$ is integrable on the interval $ℝ^{> 0}$ . Using integration by parts [8.3.1] (and a little trick) we can calculate on of its primitives by the fundamental theorem. For any $x \in ℝ^{> 0}$ we have

$\int_{1}^{x} \ln = \int_{1}^{x} 1 \cdot \ln = X \cdot \ln |_{1}^{x} - \int_{1}^{x} X \cdot \frac{1}{X} = x \cdot \ln x - \int_{1}^{x} 1 = x \cdot \ln x - x + 1$

so that $X \cdot \ln - X = X \cdot (\ln - 1)$ is (as well) a primitive of ln.
The chain rule [7.7.8] and the derivative of $| X |$ (see [7.4.3]) allow to compute

$(\ln \circ | X |)^{'} = \frac{1}{| X |} \cdot \frac{| X |}{X} = \frac{1}{X}$ ,

so that $\ln \circ | X |$ is a primitive of the complete reciprocal function $\frac{1}{X}$ .

There are further properties of the logarithm that follow immediately from its integral representation.

Proposition:

1. $\ln 1 = 0$	[8.7.2]
2. $\ln$ is strictly increasing.	[8.7.3]
3. $\ln x < 0$ for all $0 < x < 1$	[8.7.4]
4. $\ln x > 0$ for all $x > 1$	[8.7.5]

Proof:

1. ► $\ln 1 = \int_{1}^{1} \frac{1}{X} = 0$

2. ► $\ln^{'} (x) = \frac{1}{x} > 0$ for all $x > 0$ . The assertion is thus a consequence of the strict version of the monotony test [7.10.5].

3. and 4. follow directly from 1. and 2.

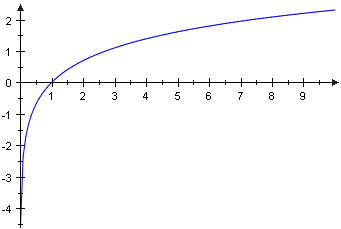From these sparse properties alone we already get quite a solid picture of the logarithm's characteristic graph. The supposed unboundedness however will only be substantiated later on when we prove that ln is bijective.

We now turn to the typical calculation rules of the logarithm, the laws of logarithms. Their proofs are essentially due to the substitution formula.

Proposition (laws of logarithms): For all $a, b \in ℝ^{> 0}$ , $n \in ℤ$ the following holds:

1. $\ln a^{n} = n \cdot \ln a$	[8.7.6]
2. $\ln \frac{1}{b} = - \ln b$	[8.7.7]
3. $\ln a \cdot b = \ln a + \ln b$	[8.7.8]
4. $\ln \frac{a}{b} = \ln a - \ln b$	[8.7.9]
5. $\ln \sqrt[n]{a} = \frac{1}{n} \cdot \ln a$ if $n > 0$	[8.7.10]

Proof:

1. ► Using the substitution formula [8.3.5] we get:

\ln a^{n} = \int_{1}^{a^{n}} \frac{1}{X} = \int_{X^{n} (1)}^{X^{n} (a)} \frac{1}{X} = \int_{1}^{a} \frac{1}{X} \circ X^{n} \cdot n \cdot X^{n - 1} = n \cdot \int_{1}^{a} \frac{X^{n - 1}}{X^{n}} = n \cdot \int_{1}^{a} \frac{1}{X} = n \cdot \ln a

2. ► With $n = - 1$ this is a special case of 1.

3. ► We employ the substitution formula a second time:

\ln a \cdot b = \int_{1}^{a \cdot b} \frac{1}{X} = \int_{b X (\frac{1}{b})}^{b X (a)} \frac{1}{X} = \int_{\frac{1}{b}}^{a} \frac{1}{X} \circ b X \cdot b = \int_{\frac{1}{b}}^{a} \frac{1}{X} = \int_{1}^{a} \frac{1}{X} - \int_{1}^{\frac{1}{b}} \frac{1}{X} = \ln a - \ln \frac{1}{b} \underset{2.}{=} \ln a + \ln b

4. ► is already done by 2. and 3.: $\ln \frac{a}{b} = \ln a \cdot \frac{1}{b} = \ln a + \ln \frac{1}{b} = \ln a - \ln b$ .

5. ► With 1. we get: $\ln a = \ln {\sqrt[n]{a}}^{n} = n \cdot \ln \sqrt[n]{a}$ , and thus the assertion.

Further properties of the logarithm are a bit more elaborate to discover. To that end we need an estimate, the so called main inequality for $\ln$ as a technical tool.

Proposition: For each $x > 0$ the value $\ln x$ could be estimated as follows:

1 - \frac{1}{x} \leq \ln x \leq x - 1

[8.7.11]

Proof: There is nothing to show if $x = 1$ . Now suppose that $x > 1$ . As $\frac{1}{t^{2}} \leq \frac{1}{t} \leq 1$ for all $t \in [1, x]$ we get the result from the integral's monotony behaviour ([8.2.10]):

- \frac{1}{x} + 1 = - \frac{1}{X} |_{1}^{x} = \int_{1}^{x} \frac{1}{X^{2}} \leq \underset{= \ln x}{\underset{︸}{\int_{1}^{x} \frac{1}{X}}} \leq \int_{1}^{x} 1 = x - 1

If $0 < x < 1$ we have $\frac{1}{x} > 1$ . Thus the just proven case applies:

\begin{array}{l} 1 - \frac{1}{\frac{1}{x}} \leq \ln \frac{1}{x} \leq \frac{1}{x} - 1 \\ \Rightarrow & 1 - x \leq - \ln x \leq \frac{1}{x} - 1 \\ \Rightarrow & x - 1 \geq \ln x \geq 1 - \frac{1}{x} \end{array}

At the very moment we only know a single value of the logarithm, namely $\ln 1 = 0$ . The main inequality now additionally provides the value at the number $e = \lim {(1 + \frac{1}{n})}^{n}$ (see [5.7.7]).

Proposition:

\ln e = 1

[8.7.12]

Proof: Consider the sequence $(\ln {(1 + \frac{1}{n})}^{n}) = (n \cdot \ln (1 + \frac{1}{n}))$ . From [8.7.11] we get

\frac{n}{n + 1} = n \cdot (1 - \frac{n}{n + 1}) = n \cdot (1 - \frac{1}{1 + \frac{1}{n}}) \leq n \cdot \ln (1 + \frac{1}{n}) \leq n \cdot \frac{1}{n} = 1

and as $\frac{n}{n + 1} \to 1$ the nesting theorem [5.5.8] yields: $\ln {(1 + \frac{1}{n})}^{n} \to 1$ . Now the continuity of ln is our final argument:

\ln e = \ln (\lim {(1 + \frac{1}{n})}^{n}) = \lim \ln {(1 + \frac{1}{n})}^{n} = 1

Surprisingly the main inequality even allows to access all values of ln. Firstly however we need a slight extension of the main inequality: Applying [8.7.11] to $\sqrt[n]{x}$ we get the estimate

n (1 - \frac{1}{\sqrt[n]{x}}) \leq \ln x \leq n (\sqrt[n]{x} - 1)

[8.7.13]

for all $x > 0$ due to [8.7.10]. Both nesting sequences prove to be convergent with the same limit:

Proposition: For all $x > 0$ we have

$\ln x = \lim n (\sqrt[n]{x} - 1)$

$\ln x = \lim n (1 - \frac{1}{\sqrt[n]{x}})$

[8.7.14]

Proof: We prove both identities simultaneously by showing that

$(n (\sqrt[n]{x} - 1))$ is convergent.
$n (\sqrt[n]{x} - 1) - n (1 - \frac{1}{\sqrt[n]{x}}) \to 0$ .

1. ► Due to [8.7.13] the sequence $(n (\sqrt[n]{x} - 1))$ is bounded from below (by $\ln x$ ). According to [5.7.1] it is thus suffucient to show that $(n (\sqrt[n]{x} - 1))$ is decreasing, i.e.

\begin{array}{l} n (\sqrt[n]{x} - 1) \geq (n + 1) (\sqrt[n + 1]{x} - 1) \\ \Leftrightarrow & n \sqrt[n]{x} + 1 \geq (n + 1) \sqrt[n + 1]{x} [+] \end{array}

for all $n \in ℕ^{*}$ . Firstly, the Bernoulli inequality
i

$1 + \frac{x - 1}{n x} \underset{[1]}{\leq} \sqrt[n]{x} \underset{[2]}{\leq} 1 + \frac{x - 1}{n}$ for all $x, n > 0$

Proof: [2] is a straight result from the common Bernoulli inequality [5.2.6]: As $\sqrt[n]{x} - 1 \geq - 1$ , we have

$x = {(1 + \sqrt[n]{x} - 1)}^{n} \geq 1 + n (\sqrt[n]{x} - 1) = 1 + n \sqrt[n]{x} - n$ ,

and thus:

$\sqrt[n]{x} \leq \frac{x + n - 1}{n} = 1 + \frac{x - 1}{n}$ .

For [1] we use the just proven result and get:

$\sqrt[n]{x} = \frac{1}{\sqrt[n]{\frac{1}{x}}} \geq \frac{1}{1 + \frac{\frac{1}{x} - 1}{n}} = \frac{n x}{n x + 1 - x} = 1 + \underset{[+]}{\underset{︸}{\frac{x - 1}{n x + 1 - x}}} \geq 1 + \frac{x - 1}{n x}$

Note that omitting the addend $1 - x$ in last step is in deed a reduction of the whole term, as the denominator of $[+]$ increases if the nominator $x - 1$ is positive, and decreases if the nominator is negative.

for the nth root yields:

n \sqrt[n]{x^{n + 1}} + 1 = n x \sqrt[n]{x} + 1 \geq n x (1 + \frac{x - 1}{n x}) + 1 = n x + x = (n + 1) x = (n + 1) \sqrt[n + 1]{x^{n + 1}}

which proves the estimate [+] when we replace x with $\sqrt[n + 1]{x}$ .

2. ► As $\sqrt[n]{x} \to 1$ (see [5.7.9]) we get the assertion from the third limit theorem [5.6.3]:

n (\sqrt[n]{x} - 1) - n (1 - \frac{1}{\sqrt[n]{x}}) = n (\sqrt[n]{x} - 1) - n \frac{\sqrt[n]{x} - 1}{\sqrt[n]{x}} = \underset{convergent}{\underset{︸}{n (\sqrt[n]{x} - 1)}} \cdot \underset{\to 0}{\underset{︸}{(1 - \frac{1}{\sqrt[n]{x}})}} \to 0

We use the result in 2. now as follows: As $(n (\sqrt[n]{x} - 1))$ is convergent, $(n (1 - \frac{1}{\sqrt[n]{x}}))$ must be convergent as well with the same limit. Due to [8.7.13] and the nesting theorem [5.5.8] this limit is $\ln x$ .

As another consequence of the main inequality we now prove that the logarithm is invertible.

Proposition: For each $y \in ℝ$ there is exactly one $x > 0$ such that $\ln x = y$ , in other words:

\ln : ℝ^{> 0} \to ℝ

is bijective.

[8.7.15]

Proof: Let $y \in ℝ$ be arbitrary. As $\ln^{'} (x) = \frac{1}{x} \neq 0$ for all $x > 0$ ln is injective due to [7.9.6], i.e. there is at most one x of the requested kind.

But there is also at least one x like this: The main inequality [8.7.11] yields $\frac{1}{2} = 1 - \frac{1}{2} \leq \ln 2$ and thus we have for any $n \in ℕ$ :

\begin{matrix} \ln 2^{2 n} = 2 n \cdot \ln 2 \geq 2 n \cdot \frac{1}{2} = n \\ \ln 2^{- 2 n} = - \ln 2^{2 n} \leq - n \end{matrix}

As $ℕ$ is unbounded in $ℝ$ there is an $n \in ℕ$ such that $\ln 2^{- 2 n} \leq - n \leq y \leq n \leq \ln 2^{2 n}$ . Now that y is in between two values of ln it is an ln-value itself according to the intermediate value theorem [6.6.2]. Thus ln is surjective as well.

In particular, [8.7.15] shows that ln is unbounded in both directions, that means $\lim_{x \to \infty} \ln x = \infty$ and $\lim_{x \to 0^{+}} \ln x = - \infty$ . The performance however is remarkably slow:

If $x \to \infty$ then ln approaches $\infty$ slower than every positive power of X, i.e. $\ln x < x^{a}$ for sufficiently large x.
If $x \to 0^{+}$ then ln approaches $- \infty$ slower than every negative power of X, i.e. $\ln x > - x^{- a}$ for sufficiently small x.

This behaviour is stated more precisely as follows.

Proposition: For each $a \in ℝ^{> 0}$ ^*) the following limits hold:

1. $\lim_{x \to \infty} \frac{\ln x}{x^{a}} = 0$	[8.7.16]
2. $\lim_{x \to 0^{+}} (x^{a} \cdot \ln x) = 0$	[8.7.17]

___________
^*) Powers with arbitrary exponents are introduced in 8.9.

Proof: We choose a number $b > 0$ such that $b < a$ , which means $a - b > 0$ , and employ the main inequality [8.7.11] again:

1. ► For all $x \geq 1$ we get:

0 \leq \frac{\ln x}{x^{a}} = \frac{1}{b} \cdot \frac{\ln x^{b}}{x^{a}} \leq \frac{1}{b} \cdot \frac{x^{b} - 1}{x^{a}} \leq \frac{1}{b} \cdot \frac{x^{b}}{x^{a}} = \frac{1}{b} \cdot \frac{1}{x^{a - b}}

But this is the assertion as $\lim_{x \to \infty} \frac{1}{x^{a - b}} = 0$ .

2. ► Now we have

0 \geq x^{a} \cdot \ln x = \frac{1}{b} \cdot x^{a} \cdot \ln x^{b} \geq \frac{1}{b} \cdot x^{a} \cdot (1 - \frac{1}{x^{b}}) = \frac{1}{b} \cdot (x^{a} - x^{a - b})

for all $0 < x \leq 1$ and in this case the assertion follows from $\lim_{x \to 0^{+}} (x^{a} - x^{a - b}) = 0$ .

In [8.1.11-12] we found an easy method to assign a primitive to functions of the type $f \cdot f^{'}$ and $\frac{f^{'}}{f^{2}}$ . The logarithm will now provide a suitable method for the $\frac{f^{'}}{f}$ type.

Proposition (logarithmic integration): If $f : A \to ℝ^{> 0}$ is differentiable then $\frac{f^{'}}{f}$ is integrable and

\ln \circ f

is a primitive of

\frac{f^{'}}{f}

[8.7.18]

Proof: $\ln \circ f$ is differentiable due to the chain rule ([7.7.8]) and the derivative claculates to

(\ln \circ f)^{'} = \ln^{'} \circ f \cdot f^{'} = \frac{1}{X} \circ f \cdot f^{'} = \frac{f^{'}}{f}

For example we have:

$\int_{0}^{1} \frac{2 X}{X^{2} + 1} = \ln \circ (X^{2} + 1) |_{0}^{1} = \ln 2 - \ln 1 = \ln 2$
$\int_{e}^{e^{2}} \frac{1}{X \cdot \ln} = \int_{e}^{e^{2}} \frac{\frac{1}{X}}{\ln} = \ln \circ \ln |_{e}^{e^{2}} = \ln (2 \cdot \ln e) - \ln (\ln e) = \ln 2$
If $x \in] - \frac{π}{2}, \frac{π}{2} [$ then $\int_{0}^{x} \tan = - \int_{0}^{x} \frac{- \sin}{\cos} = - \ln \circ \cos |_{0}^{x} = - \ln (\cos x) + \ln 1$ , so that the function $- \ln \circ \cos |] - \frac{π}{2}, \frac{π}{2} [$ is a calculated primitive of $\tan |] - \frac{π}{2}, \frac{π}{2} [$ .

8.6. 8.8.