Beispiel: Wachstum und Zerfall
0. Übersicht
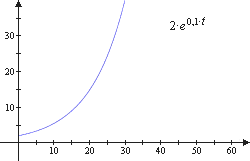
Exponentielles Wachstum:
|
|
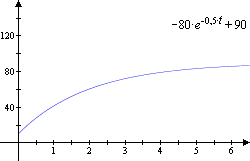
Beschränktes Wachstum:
|
|
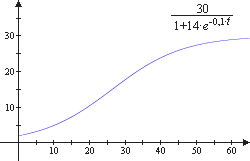
Logistisches Wachstum:
|
|
1. Exponentielles Wachstum
In der medizinischen Diagnostik gehört der Ansatz von Bakterienkulturen zu den Standardverfahren. Während einer bestimmten Phase einer solchen Kultur, kommt es zu einer wiederholten Verdopplung der Bakterienzahl nach Ablauf eines charakteristischen Zeitintervalls.
Für ein Zeitintervall von einer Stunde liegen bei einem Anfangsbestand von c Individuen etwa folgende Messwerte vor:
| Verstrichene Zeit / h |
0 |
1 |
2 |
3 |
4 |
5 |
| Individuenzahl |
c |
2c |
4c |
8c |
16c |
32c |
Offensichtlich lassen sich die jeweiligen Individuenzahlen mit Hilfe der Zweierpotenzen berechnen:
Nach n Stunden enthält die Kultur c2n viele Bakterien.
Natürlich liegt nicht nur zu jeder vollen Stunde eine Bakterienzahl vor, sondern zu jedem beliebigen Zeitpunkt. Man wird also das Wachstum der Kultur detaillierter beschreiben können, wenn man die Funktion
gegeben durch
betrachtet. Interessanterweise ist dies (auf ) die Lösung einer homogener Differentialgleichung, nämlich der Gleichung
.
Dies motiviert die folgende Definition zur Beschreibung des exponentiellen Wachstums.
|
Definition: sei (auf ) eine Lösung der homogenen Differentialgleichung
.
-
Ist , so nennen wir f eine (exponentielle) Wachstumsfunktion und a die zugehörige Wachstumskonstante.
|
[8.0.11] |
-
Ist , so nennen wir f eine (exponentielle) Zerfallsfunktion und die zugehörige Zerfallskonstante.
|
[8.0.12] |
heißt der Bestand zum Zeitpunkt t und die Wachstums- bzw. Zerfallsgeschwindigkeit zum Zeitpunkt t. Die Zahl nennen wir auch den Anfangsbestand.
|
Beachte:
f ist eine Wachstumsfunktion.
f ist eine Zerfallsfunktion.
Alle Bestandswerte, auch der Anfangsbestand , sind positiv: .
Die Äquivalenz zeigt eine zentrale Eigenschaft exponentieller Wachstums- und Zerfallsfunktionen: Zu jedem Zeitpunkt t gilt
|
Die Wachstumsgeschwindigkeit ist proportional zum Bestand.
|
[8.0.13] |
Dabei ist der konstante Proportionalitätsfaktor identisch mit der Wachstumskonstanten a.
Wachstums- und Zerfallskonstanten werden in der Dimension pro Zeiteinheit gemessen. Also z.B.
| |
(pro Sekunde) |
| |
(pro Stunde) |
| |
(pro Tag) |
| |
(pro Jahr) |
|
Beispiel: Das wöchentliche Wachstum eines Algenteppichs wird durch die Differentialgleichung
beschrieben. Nach welcher Zeit ist ein ursprünglich großer Teppich auf angewachsen?
Lösung: Für die zugehörige Wachstumsfunktion hat man: . Zu lösen ist daher die Gleichung
|
Die Zeit T, die ein Wachstumsprozess benötigt um seinen Anfangsbestand zu verdoppeln, ist ein übersichtliches Maß zum Vergleich verschiedener Wachstumsprozesse. Sie läßt sich (unabhängig vom Anfangsbestand!) leicht über die Wachstumskonstante a bestimmen:
Parallel dazu benögt ein Zerfallsprozess Zeiteinheiten um seinen Bestand zu halbieren:
.
Wir setzen daher fest:
|
Definition:
-
Ist f eine Wachstumsfunktion, so heißt die Zahl
|
[8.0.14] |
die Verdopplungszeit von f.
-
Ist f eine Zerfallsfunktion, so heißt die Zahl
|
[8.0.15] |
die Halbwertzeit von f.
|
Für unser Eingangsbeispiel ergibt sich also mit eine Verdopplungszeit von einer Stunde.
Beachte:
|
| ► |
|
| ►
|
Der Bestand verdoppelt, bzw. halbiert sich zu jedem Zeitpunkt t nach Ablauf der Zeit T, also nicht nur zu Beginn () des Prozesses, denn für eine Wachstumsfunktion etwa hat man bei beliebigem t:
|
|
Beispiel: Die Halbwertzeit von Radium 226 beträgt ungefähr 1620 Jahre. Nach wie vielen Jahren sind 80% einer Ausgangsmenge dieses Elements zerfallen?
Lösung: Wir benötigen die zugehörige Zerfallsfunktion und berechnen dazu zunächst die Zerfallskonstante:
.
Nach Ablauf der gesuchten Zeit t (in Jahren) sind nur noch 20% der Ausgangsmenge vorhanden, daher ist t bestimmt durch die Bedingung
|
In der Physik findet man viele "klassische" Anwendungsbereiche für Zerfallsfunktionen. Der gerade im Beispiel betrachtete radioaktive Zerfall ist sicherlich das bekannteste. Weitere physikalische Beispiele sind:
Die Abnahme von Strahlungsintensitäten (Röntgenstrahlen etwa verlieren beim Durchgang durch Bleischirme an Intensität, Laserstrahlen beim Durchgang durch ein Medium). Der Rückgang des Luftdrucks mit steigender Höhe wird durch die Barometrische Höhenformel
beschrieben. Die Datierung archäologischer Funde durch die Radiokarbon-Methode (C-14-Methode): Natürlicher Kohlenstoff enthält einen konstanten Anteil des radioaktiven Iosotops 14C. Durch Austauschprozesse wird dieser Anteil auch in lebenden Organismen konstant gehalten. Nach dem Tod verringert er sich jedoch stetig, da der Zerfall nicht durch Neuaufnahmen kompensiert werden kann.
Wir berechnen als Beispiel das Alter eines Holzbalkens, der pro Minute 8 Entladungsimpulse 14C pro g Kohlenstoff abgibt. Bei frischem Holz beträgt dieser Wert 15,3. 14C hat eine Halbwertzeit von 5760 Jahren, also eine Zerfallskonstante von . Wir messen also mit
die Anzahl der Entladungsimpulse pro Minute und Gramm zum Zeitpunkt t (in Jahren). Über die Gleichung
erhalten wir als Lösung ein Alter von ca. 5390 Jahren.
2. Beschränktes Wachstum
Nicht jeder Wachstumsprozess kann exponentiell verlaufen, d.h. die Bedingung [8.0.13] erfüllen. Die Temperatur einer Flüssigkeit etwa, die in einem ideal isolierten Behälter von einer Heizspirale mit konstanter Oberflächentemperatur aufgewämt wird, kann nicht beliebig hoch steigen, sondern wird durch beschränkt sein.
Auch wird die Aufwärmgeschwindigkeit nicht proportional zur bestehenden Temperatur sein, sondern - ganz im Gegenteil - sie wird um so kleiner sein, je niedriger die Temperaturdifferenz ist, sie ist also proportional zu . Der Temperaturverlauf in der Flüssigkeit läßt sich daher durch die inhomogene Differentialgleichung
beschreiben.
|
Definition: Die Lösungen der inhomogenen Differentialgleichung
|
[8.0.16] |
nennen wir beschränkte Wachstumsfunktionen.
|
Nach [8.11.6] sind die Lösungen von [8.0.16] gegeben durch
, man hat also:
f ist eine beschränkte Wachstumsfunktion .
gibt dabei offensichtlich das Supremum (bzw. Infimum) des Bestands an.
Der im Eingangsbeispiel gesuchte Temperaturverlauf läßt sich also durch beschreiben. Für , und ist diese Funktion in der Übersicht skizziert.
Das folgende Beispiel zeigt, dass man die Osmose als einen beschränkten Wachstumsprozess auffassen kann.
Die Vertreter der Gattung Chaetopterus sind bodenbewohnende Röhrenwürmer der Meere. Die Salzkonzentration ihrer Eier ist identisch mit der des umgebenden Seewassers. Legt man ein solches Ei in verdünntes Seewasser, so wird durch osmotischen Druck so lange Wasser in die Eizelle einströmen bis die Salzkonzentrationen wieder ausgeglichen sind.
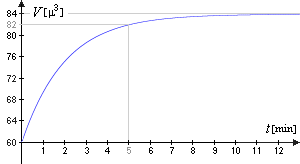
Die folgende Grafik zeigt die damit verbundene Volumenzunahme: |

Chaetopterus variopedatus |
|
Dieser Verlauf läßt sich gut durch eine beschränkte Wachstumsfunktion beschreiben, denn die Geschwindigkeit der Volumenzunahme ist direkt proportional zur Differenz der Salzkonzentrationen.
Mit und hat man also
,
|
und die Information liefert . Also ist
.
Wenngleich die Osmose in vielen biologischen Systemen eine entscheidende Bedeutung hat, so ist sie doch ein rein physikalisches Phänomen. Überhaupt findet man in der Physik viele Anwendungsbeispiele für beschränkte Wachstumsfunktionen, wie etwa die Beschreibung der Abkühlung eines heißen Körpers oder der Entladung eines Kondensators.
3. Logistisches Wachstum
Während die physikalischen Beispiele i.a. recht exakt durch unsere mathematischen Überlegungen beschrieben werden, trifft dies auf andere Anwendungen, wie etwa in der Biologie, nur eingeschränkt zu.
Die Bakterienkultur aus dem Eingangsbeispiel wird sich nur in einer bestimmten Phase ideal verhalten, so dass die notierte exponentielle Wachstumsfunktion nur für einen begrenzten Zeitraum eine gültige Beschreibung liefert. So wird etwa die Größe der Petrischale, der Vorrat an Nährstoffen und die Ansammlung von toxischen Stoffwechselprodukten zu einem begrenzenden Faktor beitragen, der um so stärker ins Gewicht fällt, je größer die Population ist
Die Wachstumsgeschwindigkeit wird also nicht starr proportional zum Bestand sein, sondern einen variablen, vom aktuellen Bestand abhängigen Proportionalitätsfaktor aufweisen. Dieser Faktor muss mit steigender Population immer kleiner werden, und an der oberen Kapazitätsgrenze des Bestands, der Tragfähigkeit der Population, den Wert 0 haben.
Als ein erstes Beispiel für einen solchen Faktor führt der belgische Mathematiker Pierre François Verhulst 1846 den Ausdruck ein. Für Bestandswerte weit unterhalb der Tragfähigkeit liefert er Werte nahe bei a, hat der Bestand seine Tragfähigkeit erreicht - -, ist der Faktor gleich Null. Die modifizierte Differentialgleichung, die Verhulstgleichung
ist allerdings nicht mehr linear. Mit Hilfe der
logarithmischen Integration
i  |
|
ist eine Stammfunktion zu
|
jedoch können wir auch diese Gleichung lösen, zumindest für Bestände, die ihre Tragfähigkeit nie erreichen.
|
Definition: Es sei . Die Lösungen der Differentialgleichung
|
[8.0.17] |
nennen wir logistische Wachstumsfunktionen.
|
Mit der Abkürzung zeigen wir jetzt:
f ist eine logistische Wachstumsfunktion
Logistische Wachstumsfunktionen sind also insbesondere beliebig oft differenzierbar.
Beweis: Wir lösen dazu die Gleichung [8.0.17], also die Gleichung
Funktionen auf Intervallen mit konstanter Ableitung sind linear, also hat man
wobei
i  |
|
nach Einsetzen von 0
|
.
Also gilt für alle :
Als Beispiel modifizieren wir unsere Algen-Aufgabe aus Teil 1:
|
Beispiel: Der Algenteppich aus dem ersten Beispiel (Wachstumskonstante (pro Woche) und Anfangsbestand ) entwickelt sich in einem großen Abwasserbecken mit konstanter Nährstoffzufuhr. Dadurch ändert sich die Wachstumskonstante nicht, so dass einzig die Tragfähigkeit ein einschränkender Faktor ist.
Lösung: Mit wird also das logistische Wachstum beschrieben durch
Man beachte, dass der Wert zwar noch relativ nah bei 4,45 liegt, sich aber bereits eine Verlangsamung des exponentiellen Verlaufs einstellt. Man vergleiche dazu auch die beiden Grafiken am Anfang der Seite!
|
Logistische Wachstumsfunktionen vermitteln zwischen beschränktem und exponentiellem Wachstum, denn die Lösung der Verhulstgleichung verhält sich für Bestandswerte
-
nahe der Tragfähigkeit, also , ähnlich wie die Lösung von .
-
weit entfernt von der Tragfähigkeit, d.h. , ähnlich wie die Lösung von .
Wir beschäftigen uns nun etwas intensiver mit logistischen Wachstumsfunktionen und stellen einige ihrer Eigenschaften zusammen.
|
Bemerkung: Für eine logistische Wachstumsfunktion, d.h. , gilt:
-
f ist streng monoton steigend.
|
[8.0.18] |
-
Ist , so ist .
|
[8.0.19]
|
|
Zu diesem Zeitpunkt erreicht der Bestand die Hälfte seiner Tragfähigkeit mit maximaler Wachstumsgeschwindigkeit.
|
Beweis:
1. ► Mit hat man und da a und
ohnehin positiv sind, gilt für alle :
,
so dass der Monotoniesatz [7.10.5] die Behauptung liefert.
2. ► Die erste Behauptung ergibt sich aus der Abschätzung
.
Da f beliebig oft differenzierbar ist, stehen uns zur Betrachtung der Maximalstellen von das notwendige ([7.9.2]) und das hinreichende ([7.9.17]) Kriterium zur Verfügung. Wir berechnen daher
.
Nach dem Beweis zu 1. ist stets von 0 verschieden, also hat man:
.
Für ein solches t ist dann
.
Schließlich haben wir: .
|
Um zu prüfen, ob beobachtete Daten zu einem logistischen Prozess gehören, ist es hilfreich, die Parameter einer logistischen Wachstumsfunktion einstellen zu können.
|
Bemerkung: Ist f eine logistische Wachstumsfunktion, also , so gilt für alle :
-
|
[8.0.20] |
-
|
[8.0.21] |
-
|
[8.0.22] |
Beweis: 1. ist offensichtlich.
2. ► Mit erhält man aus 1.:
Man beachte, dass aufgrund der strengen Monotonie , und damit nach [0] auch der Nenner , ungleich 0 ist.
3. ► Mit den Abkürzungen
haben wir zunächst ( f ist streng monoton), so dass bei den folgenden Rechnungen alle Nenner von 0 verschieden sind. Aus 2. ergibt sich für die quadratische Gleichung
die wegen
von 1 gelöst wird, so dass man die folgende Zerlegung in Linearfaktoren konstruieren kann:
Da niemals gleich 1 ist, muss gelten, womit die Behauptung
gewonnen ist.
|
Der offiziellen UN Statistik entnehmen wir die folgenden Daten über die Größe der Weltbevölkerung (in Tausend):
| 1950: | 2 532 229 |
| 1975: | 4 076 419 |
| 2000: | 6 122 770 |
Unterstellt man logistisches Wachstum, d.h. , so bedeutet dies mit 1950 als Startjahr
Mit [8.0.22/21/20] errechnet man damit der Reihe nach
Die Tragfähigkeit unserer Population beträgt in diesem Modell also ca. 15,65 Milliarden, wobei ihre Hälfte nach Jahren, also etwa 2018, erreicht sein wird.
Ob dieses Modell eine zuverlässige Prognose für die künftige Entwicklung gestattet, hängt natürlich davon ab, wie realistisch die Annahme des logistischen Wachstums ist, bzw. bleiben wird. |
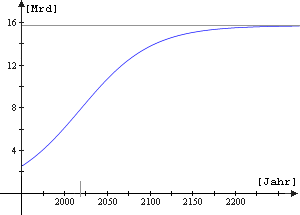 |
Immerhin aber liegt unser Wert recht nahe bei UN Schätzung (high variant) von 10.614.318 für das Jahr 2050! Und selbst die Zahl 15.804.873 für das Jahr 2100 überschreitet unsere berechnete Tragfähigkeit um weniger als 1%.
Umfangreiche Datensätze und weitere Informationen zur Entwicklung der Weltbevölkerung findet man auf der Lernseite World Population Resources.
|